Research
Partial Differential Equations on Surfaces
PDEs posed on surfaces are essential in modeling of processes occurring on or within thin membranes or interfaces. The fact that in these applications the transversal dimension of the domain is negligibly small compared to the other two results in geometric effects having strong influence on the physics of the phenomena. It is therefore natural to model them using PDEs posed on surfaces rather than PDEs posed in a very thin 3D domain.
There are three main aspects of research in this field:
- Modeling: deriving PDEs based on physical laws,
- PDE theory: establishing existence (and uniqueness) of solutions to PDEs on surfaces,
- Discretization: designing, implementing and analyzing finite element schemes for the PDEs.
What I am primarily concerned with is how to discretize such PDEs in a robust way. I have also worked a little bit on the surface PDE theory.
My research
Inf-Sup Stability of Parabolic TraceFEM
This is joint work with
- Lucas Bouck (Carnegie Mellon University),
- Ricardo H. Nochetto (University of Maryland, College Park),
- Vladimir Yushutin (University of Tennessee, Knoxville).
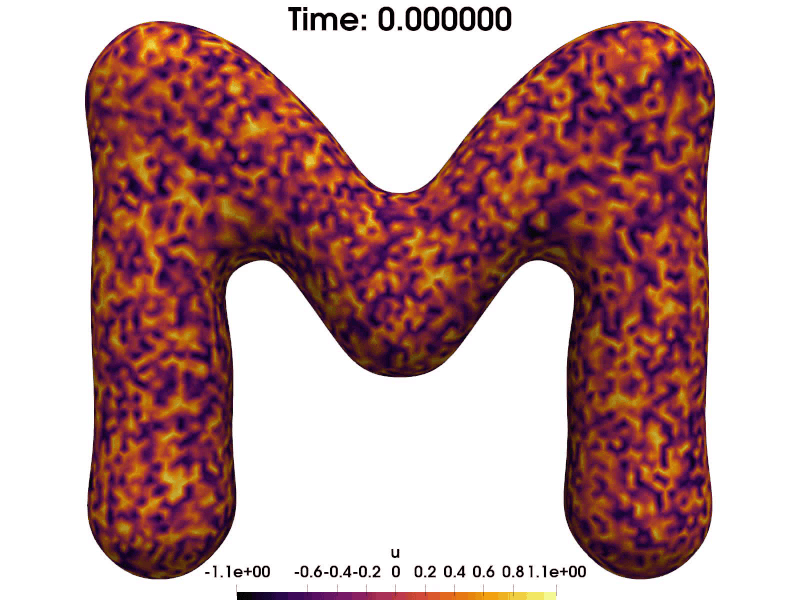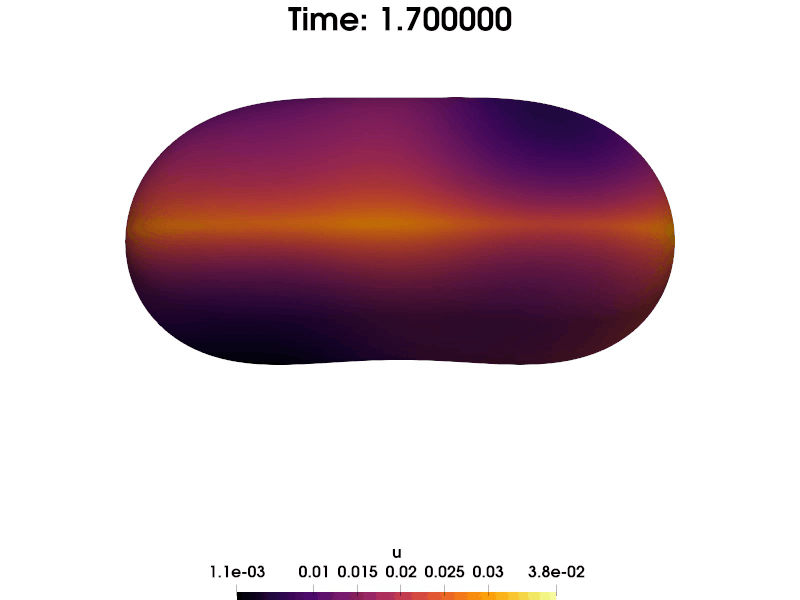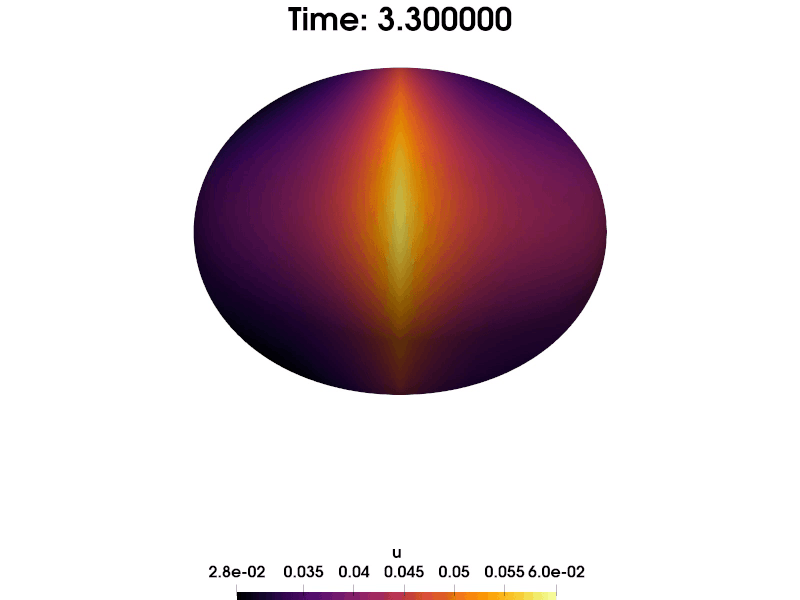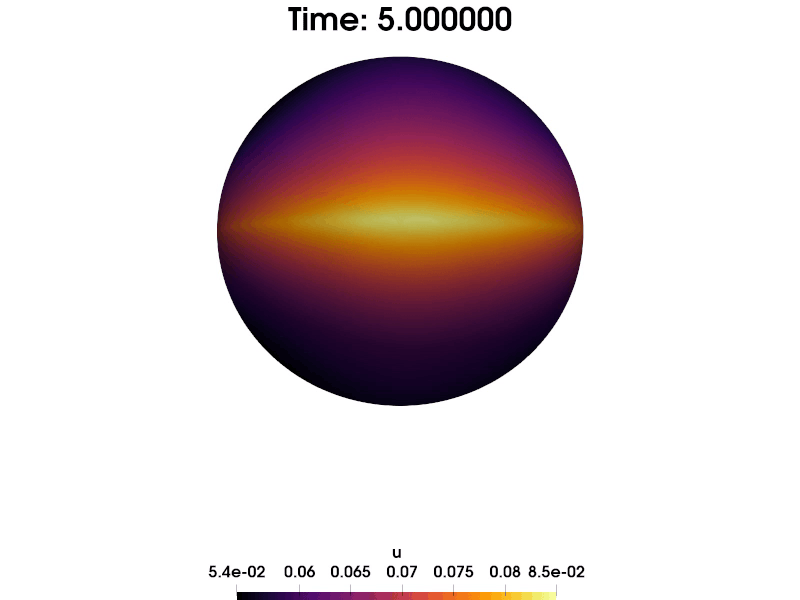
We consider the heat equation $\partial_t u - \Delta_\Gamma u = f, u(0) = u_0$ posed on a stationary surface $\Gamma$. In this work, we discretize the problem in space with an Eulerian finite element method called TraceFEM and derive necessary and sufficient conditions for the uniform discrete inf-sup stability of the scheme. We relate the inf-sup stability of the scheme with the $H^1$-stability of an appropriate $L^2$-projection on the finite element space. With the inf-sup stability at hand, we were able to derive a quasi-best approximation property, optimal order-regularity error estimates and convergence under minimal data regularity: $u_0 \in L^2, f \in L^2([0,T]; H^{-1})$. The proposed method also yields an optimal condition number when discretized further in space.
The work was motivated by discretization of a hydrodynamical model of liquid crystals (the surface Beris-Edwards model) that was recently derived by my coauthors. In that problem, due to its nonlinear structure, proving convergence of the scheme requires having a priori control of the time derivative of the discrete solution. However, due to the model’s complex structure, obtaining a priori stability estimates by testing with $\partial_t u$ is not possible. Simplification of the problem led to the quesiton of convergence of TraceFEM for the simple heat equation $\partial_t u - \Delta_\Gamma u = f, u(0) = u_0$ under minimal data regularity. Existing methods in the literature did not yield that result, which was the catalyst for the present work.
The paper is to appear in Journal of Foundations of Computational Mathematics.
arXiv: https://arxiv.org/abs/2409.13944
$L^p$-based Soboled Theory for PDEs on Closed Manifolds of Class $C^m$
This is joint work with
- Gonzalo A. Benavides (University of Maryland, College Park),
- Ricardo H. Nochetto (University of Maryland, College Park).
PDEs posed on surfaces (or more generally manifolds) has been a topic of research interest for many decades. However, the vast majority of the work in this field has been for manifolds that are smooth (i.e., Riemannian manifolds). This simplifying assumption enables using very powerful analytical tools (e.g., potential theory). However, in real-life applications, the manifolds in question are never smooth. It is therefore desireable to have a PDEs theory that is compatible with non-smooth manifolds (e.g. of class $C^k, k \geq 1$) and that is elementary. This work tackles these issues.
In particular, for closed manifolds of class $C^k$, we study the four main problems:
- the Laplace-Beltrami problem,
- the Bochner-Laplace problem (a tangential vector Laplace problem),
- the tangent surface Stokes, and
- tangent surface Navier-Stokes problems.
For these problems, we address the following questions:
- Well-posedness in $W^{1,p}, 1<p<\infty$.
- $W^{k,p}$-regularity estimates.
In all these results, we focus on having sharp assumptions on the regularity of the underlying manifold $\Gamma$. We develop this theory without resorting to the potential theory on manifolds. Instead, we use the Calderon-Zygmund theory in Euclidean domains and combine it with geometric and functional-analytic arguments.
arXiv: https://arxiv.org/abs/2508.11109
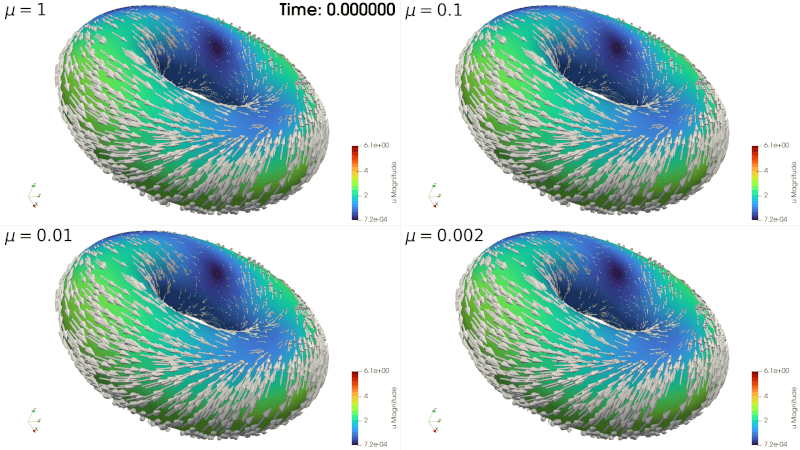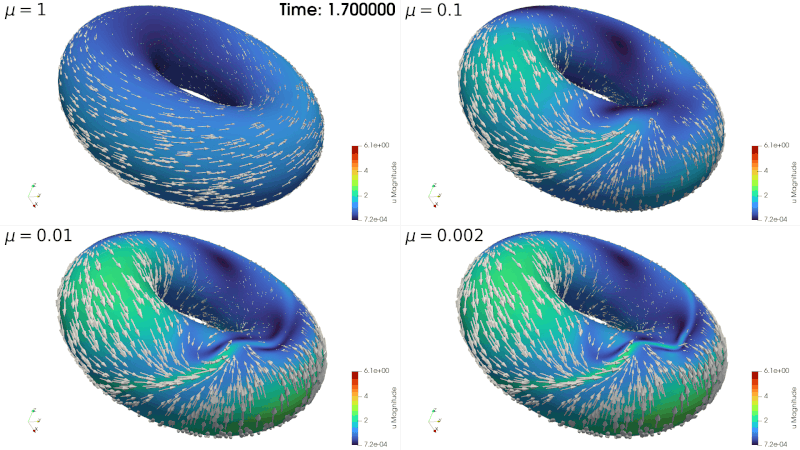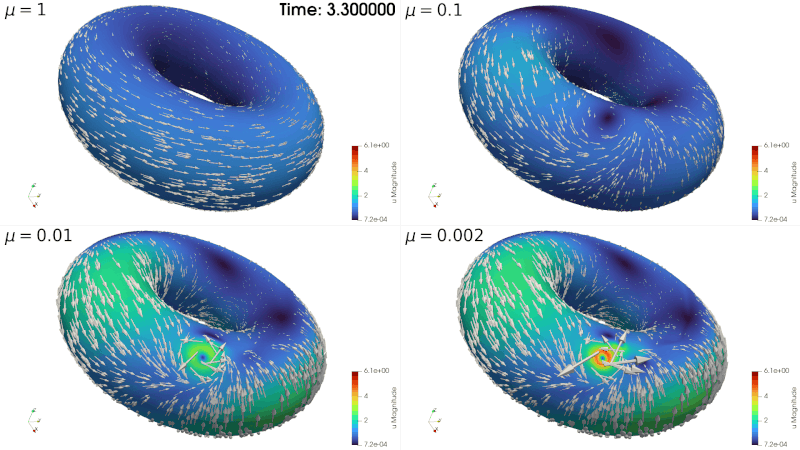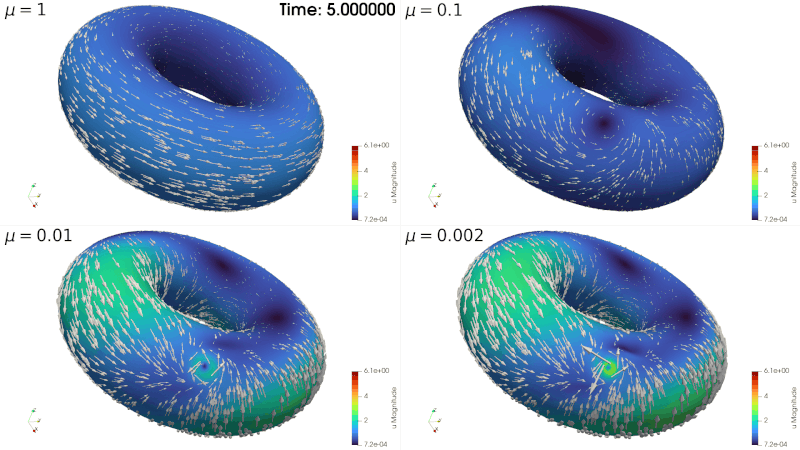
Surface Stokes Without Inf-Sup Condition
This is joint work with
- Ricardo H. Nochetto (University of Maryland, College Park).
In bounded, flat domains, finite element discretization of the Stokes problem generally involves verifying the discrete inf-sup condition (also known as the Babuška-Brezzi condition). Practically, this puts a constraint on the polynomial degrees that can be used for the velocity and the pressure variables.
In the present work we show that the tangent Stokes problem posed on a closed manifold can be reformulated as an elliptic problem in the velocity-pressure pair-variable. We prove that the resulting non-coercive elliptic problem is well-posed. This then leads to a family of numerical methods that do not require the validity of the discrete inf-sup condition by the virtue of being a discretization of an elliptic problem (as opposed to a saddle point one). We derive stability and quasi-best approximation property, as well as error estimates for a parametric FEM. We provide numerical experiments that demonstrate the efficiency of the new method.
The manuscript is submitted.
arXiv: https://arxiv.org/abs/2508.13342